이 게시물은
1. 모두를 위한 메타러닝
2. 파이썬과 케라스를 이용한 딥려닝/강화학습 주식투자
를 참고하였다.
강화학습은 에이전트가 환경과 상호작용하며서
보상을 최대화하도록 에이전트의 신경망을 학습하는 머신러닝 방법이다.
위의 사진에서 호랑이가 에이전트라면 자연이 환경이고
멧돼지고기를 먹음을 통해 얻는 허기의 해소가 보상이다.
이러한 자연의 원리를 아래와같은 그림으로 모델링할 수 있다.
마르코프 가정
다음 식을 보자
$P(x_t | x_1, x_2, ..., x_{t-1}) = P(x_t | x_{t-1})$
위 식은 우주의 인과율을 수학으로 모델링한 것이다.
현재 시간 $t$의 상태를 이전에 일어난 원인들이 결정할 수 있다.
$x_1$이라는 사건은 $x_2$라는 사건을 야기할 수 있다.
$x_2$라는 사건은 $x_3$라는 사건을 야기할 수 있다.
예를들어 무리한 볼링은 손의 근육통을 유발할 수 있다.
손의 근육통이 심할 경우 한 동안은 볼링장에 가지 않는 결과를 유발할 수 있다.
이런식으로 어떤 사건은 어떤 사건이라는 결과를 야기할 수 있고
결과로 인한 사건은 또 다른 사건을 위한 원인이 될 수 있다.
그러나 최종사건인 볼링장에 가지 않는 결과를 생각할 때
볼링장에 가지 않는 원인인 손 근육통만을 고려해도 문제 없다.
마르코프 가정은 이와 같이
$P(x_t | x_1, x_2, ..., x_{t-1})$를 $P(x_t | x_{t-1})$와 같이
단순화 할 수 있다.
$P(x_t | x_{t-1})$은 상태 전이 확률(state transition probability)이다.
연속적인 사건들간의 인과관계를 생각해보자.
지구에 도달하는 태양열은 물을 증발시키는 원인이 된다.
물이 증발되어 일정량이 성층권에 도달하는 것은 구름이라는 결과를 야기한다.
구름에 일정량의 수증기가 쌓이면 구름속에서 수증기들이 응집되어 중력의 영향을 크게 받게되어
땅으로 빗물로서 떨어지게 된다.
어떤 빗물이 식물의 뿌리에 떨어질 경우 식물이 흡수할 양분이 되지만
도시의 도로에 떨어질 경우 출퇴근길을 힘들게 만드는 원인이 된다.
(위의 두 경우에서 알 수 있듯이 자연에서 일어나는 일은 인간이 관찰했을 때 확률적인 특성이 있다.)
마르코프 결정과정
위와는 다른 성격의 연속적인 사건들간의 인과관계가 있다.
바로 지적존재의 행동으로 인한 인과관계이다.
다람쥐가 숲을 돌아다니는 중이다.
숲을 돌아다니다 우연히 도토리 나무에 도달했다.
도토리나무의 도토리 냄새가 다람쥐의 후각을 자극하였고
다람쥐는 본능에 이끌려 도토리를 먹었다.
처음먹어보는 도토리는 너무 맛있었다.
다람쥐는 도파민을 보상으로 받았고
다람쥐의 변한 도파민 체계는 도토리를 계속 탐하게 되었다.
다람쥐가 다시 한번 도토리를 발견했을 때
맛있는 느낌을 느끼기 위해
도토리를 또 먹었다.
위와 같은 사건에서
우연히 확률적으로 다람쥐가 도토리를 발견하여
도토리를 먹고 맛있는 느낌이 들었던 것이 원인이 되어
다람쥐의 도파민 체계를 변화시키는 결과를 낳았고
다람쥐의 도파민 체계의 변화가 원인이 되어
다람쥐가 도토리를 탐하게 되는 결과를 낳았고
다람쥐가 도토리를 탐하게 된 것이 원인이 되어
다람쥐가 도토리를 다시 발견했을 때
도토리를 또 먹게되는 결과를 낳았다.
강화학습은 이와같이 환경과 상호작용함으로 인한 인과관계를
수학으로 모델링하여 기계학습에 적용한 것이다.
지적존재를 강화학습이라는 전문분야에서는 에이전트라고 한다.
아래 그림처럼 강화학습은 에이전트와 환경과의 상호작용으로인한
에이전트의 학습이라고 할 수 있다.
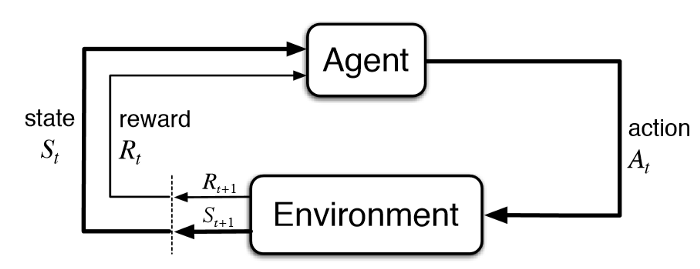
이와같은 경우는 수학적으로 아래와 같은 마르코프 결정과정으로 모델링 할 수 있다.
마르코프 결정 과정 = $(S, A, P, R, \gamma)$
$S$ : 상태집합 - 에이전트가 맞딱드리는 상황
$A$ : 행동집합 - 에이전트가 취할 수 있는 행동
$P$ : 변환확률 - 행동으로 인한 결과로서 나타나는 상태의 확률
$R$ : 보상함수 - 행동을 취했을 때 환경으로부터 받는 보상
$\gamma$ : 감가율 - 무제한의 시간동안 학습이 진행될 때 보상이 과하게 커지는 것을 막는 인자
위의 그림을 봤을 때
상태 $S_t$를 관찰한 에이전트는 적절한 행동 $A_t$를 취하고
적절한 행동으로 인해 환경이 변하게 된다.$S_{t+1}$
(컵이 찬장의 1층에 있는 상태에서 컵을 집어 찬장의 2층으로 옮기는 행동을 취하면
컵이 찬장의 2층에 있는 상태가 된다.)
적절하게 취한 행동이 에이전트에게 유익한 상태를 만들경우
에이전트는 유익한 상태에서 보상$R_{t+1}$을 얻는다.
아래 그림을 다시 보자.

보상 $R_t$를 입력받은 에이전트는 보상에 대한 경험을 통해
보상을 더 잘 얻기 위해 행동$A_t$를 수행하려고 노력할 것이다.
보상으로 인해 에이전트가 변했기 때문이다.
에이전트의 내부에서 어떤 일이 일어나는 것일까?
정책함수
다람쥐의 예를 들었을 때
이전 도토리로 인한 보상을 얻은 다람쥐가
다시 한 번 우연히 도토리를 맞딱드리는 상황은 상태$S_t$이다.
에이전트는 상태를 관찰하고 그에 따라 적절한 행동$A_t$를 취한다.
이 과정을 수학적으로
$\pi_\theta(a_t|s_t)$와 같이 나타낼 수 있다.
이 확률식을 정책 함수라고 한다.
그리스 알파벳 $\pi$는 policy의 p이다.
에이전트가 사건
$s_1$을 마주쳤을 때 $s_1$에 적절한 행동$a_1$이 있고
$s_2$를 마주쳤을 때 $s_2$에 적절한 행동$a_2$가 있다.
이런식으로 연속적으로 마주치는 사건들과 그 사건들에 적절한 행동 쌍을
다음과같은 식으로 나타낼 수 있다.
$\tau = (s_1, a_1, ..., s_T, a_T)$
위의 배열을 trajectory라고 하며
그리스 알파벳 $\tau$는 trajectory의 t이다.
trajectory에 대한 확률분포를 다음과같이 나타낼 수 있다.
$p_\theta(\tau) = p(s_1)\Pi^T_{t_1}\pi_\theta(a_t|s_t)p(s_{t+1}|s_t, a_t)$
trajectory에 대한 확률분포는
첫번째 상태의 확률 $\times$ (정책함수 $\times$ 변환확률)
이다.
이 확률분포는 다음같은 목적함수를 통해 최적화한다.
$\theta^* = argmax_\theta \mathbb{E}_{\tau \sim p_\theta(\tau)}[\Sigma_t r(s_t, a_t)]$
이 식은 보상함수 $r(s_t, a_t)$의 합에 대한 기댓값을 최대화하는 $\theta$를 찾는 식이다.
'인공지능' 카테고리의 다른 글
| SNAIL (0) | 2023.01.31 |
|---|---|
| 강화학습 기본2 (0) | 2023.01.31 |
| 다양한 심층강화학습 방법 소개(Adaptation, Generalization관점) (0) | 2023.01.30 |
| Habitat 2.0 (0) | 2023.01.27 |
| Common Objects in 3D (0) | 2023.01.27 |



