Long-term episodic memory networks는
아래 그림과 같이 세 가지 종류가 있다.

제한된 메모리에서 중요하지 않은 부분, noisy 데이터를 포함하는
긴 데이터 스트림으로부터 학습하는 문제를 푸는 모델이다.
에이전트 $mathcal{A}$는
스트리밍 데이터$X = {x_1,...,x_T}$를 입력받고
외부 메모리 $M = [m_1, ..., m_N], m_i \in \mathbb{R}^d$, $T \gg N$를 관리한다.
강화학습에서는 정책함수를 다음과같이 정의한다.
$\pi(a_t|s_t)$
행동 $a_t$를 지워야 할 메모리 셀이라고 간주한다.
$s_t = [M_t; x_t]$ : 상태
$M_t$ : 현재 메모리
$x_t$ : 시간 $t$에서 입력
메모리가 가득 찼을 때
에이전트는 $x_t$를 추가하기 위해 다음 정책함수에 기반해서 메모리를 지운다.
$\pi(m_i|M_t, x_t)$
다음 식은 각 메모리의 기억 값이다.
$1 - \pi(m_i|M_t, x_t)$
임의의 타임 스텝 $t_f$에
보상 $\mathcal{R}_\mathcal{T}$와 함께 태스크 $\mathcal{T}$를 마주친다.
타임스텝 $t$에 도착하는 $x_t$는 메모리 벡터 representation $e_t \in \mathbb{R}^d$
Memory-Retention Mechanisms
그림에서 볼 수 있었던 세 memory-retention mechanisms에 대해 설명한다.
입력 $x_t$와 각 메모리 셀 $m_{t,i}$을 vector representation으로 인코딩한다.
$c_t = \psi(x_t)$
$e_{t, i} = \varphi(m_{t, i})$
$c_t, e_{t, i} \in \mathcal{R}^d$일 때
$\psi(\cdot)$은 RNN controller와 비슷한 입력 임베딩 또는 포지션 임베딩이 될 수 있다.
$\varphi(\cdot)$은 기본 외부 메모리의 메모리 인코딩 층이 될 수 있다.
Input-Matching LEMN

3가지 중 가장 단순한 매커니즘이다.
각 메모리 representation $m_i$는 $m_i$와 현재 입력 $x_t$ 사이의 학습된 유사도로 계산된다.
logit $z_i$의 지수적 움직임 평균 $v_t$를 계산해 최근에 사용된 LRU 주소화를 한다.
LRU factor $\gamma_t$와 정책은 다음과 같다.

$W_\gamma \in \mathbb{R}^d, b_r \in \mathbb{R}$
Spatial LEMN

IM-LEMN의 주요 결점은 각 메모리의 점수가 입력 $x_t$에만 의존한다는 것이다.
다시 말해서 점수는 메모리 셀과 입력 사이에서 독립적으로 계산된다.
그러나 이것의 메모리의 다른 데이터 인스턴스들에 대한 상대적 중요성은 생각하지 않는다.
이런 한계를 극복하기 위해서 spatial LEMN이 제안되었다.
이 모델은 양방향 GRU를 사용하는 이웃, 다른 메모리 셀들에 대한 메모리 셀들의 상대적 중요성을 계산한다.

$W_f \in \mathbb{R}^{2d \times d}, d_f \in \mathbb{R}^d$
스칼라 출력을 출력하는 MLP는 정책을 계산한다.

$W_h \in \mathbb{R}^{d \times d/4}, b_h \in \mathbb{R}^{d/4}, W_g \in \mathbb{R}^{d/4}, b_g \in \mathbb{R}$
메모리셀의 일반적 중요성과 IM-LEMN에 대조되는 이웃사이의 관계
Spatio-Temporal LEMN
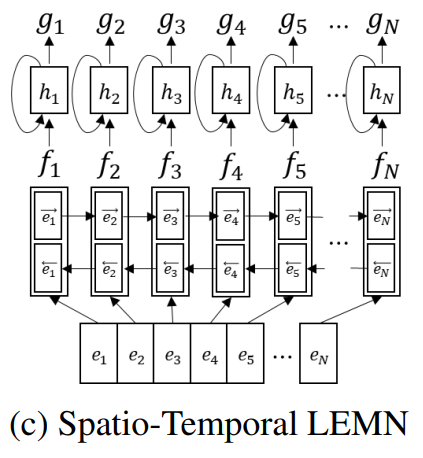
에피소딕 태스크들에서 메모리의 중요성은 시간과 태스크들에 따라 바뀐다.
GRU를 사용하는 Spatio-Temporal LEMN이 제안되었다.
이 모델은 시간에 따라 역사적 중요성을 고려한다.

Memory Update
앞서 언급한 memory-retention mechanism을 사용해서, 에이전트는
다음 확률 분포 $\pi(m_i|M_t, x_t)$에서 $i$번째 메모리 셀을 샘플링한다.
그 다음에 $i$번째 메모리 셀을 지우고 입력 $x_t$를 추가한다.
$M_{t+1} = [m_1, \cdot\cdot\cdot, m_{i-1}, m_{i+1}, \cdot\cdot\cdot, m_N, x_t]$
'인공지능' 카테고리의 다른 글
| 메타비지도학습 CACTUs (0) | 2023.02.02 |
|---|---|
| 메타지도학습 (0) | 2023.02.02 |
| 엔드 투 엔드 메모리 네트워크 (1) | 2023.02.01 |
| 메모리 네트워크 (0) | 2023.01.31 |
| SNAIL (0) | 2023.01.31 |



